Software Engineering Tools for Matrix Block Encoding
In my article about the Math Perspective on Block Encoding, I briefly introduced the theoretical background and motivation for matrix block encoding. Block encoding is a technique used to input a non-unitary matrix A into a quantum computer by embedding it into a unitary operator. In this article, I focus on the practical aspect of block encoding — I’ll explore several libraries that can be used to construct a block encoding of a matrix in practice.
Prerequisites. Familiarity with the block encoding concept, linear algebra, quantum computing, Python programming language, and/or MATLAB.
Block Encodings of Certain Sparse Matrices
I will begin with the block encoding of sparse matrices with a particular structure. The algorithm to block encode sparse matrices with a particular structure was developed by researchers at Lawrence Berkeley National Laboratory (Quantum Computing Lab) and is written in MATLAB. It uses the QCLAB tool, which is a MATLAB implementation for quantum circuit simulation that includes a quantum logical gates implementation. The algorithm supports only 2-by-2 symmetric matrices, circulant matrices, and binary tree matrices. If you’re interested, you can find the code for the algorithm on GitHub at this link.
Let’s try out this compact framework for block-encoding a matrix. First, we need to install QCLAB to construct a quantum circuit for the matrix block encoding. I can easily do this by cloning the repository from GitHub:
git clone https://github.com/QuantumComputingLab/qclab.gitand then adding all files to MATLAB path
addpath(qclabroot);
savepath;Example 1. Let’s block encode the following 2-by-2 symmetric matrix
To do so, I have to provide the diagonal and off-diagonal elements into the function realsym2() to construct the circuit corresponding to the block encoding and the corresponding matrix:
diagonal = 0.2;
off_diagonal = 0.6;
circuit = realsym2(diagonal, off_diagonal);To display unitary for the block encoding, I can use the .matrix attribute:
unitary = circuit.matrix;To display the quantum circuit, there is an associated method .draw() for the circuit object
circuit.draw();
┏━━┓ ┏━━┓
q0: ━━━━━┫RY┣━⊕━┫RY┣━⊕━━━━━━━
┗━━┛ ┃ ┗━━┛ ┃
┏━┓ ┃ ┃ ┏━┓
q1: ━┫H┣━━━━━━●━━━━━━●━●━┫H┣━
┗━┛ ┃ ┗━┛
┃
q2: ━━━━━━━━━━━━━━━━━━━⊕━━━━━Example 2.
Similarly, I could block encode a 3-sparse circulant matrix using tridiag_cab() function.
To do so, I need to specify the size of the matrix as base 2: n = 3 and pass in to the function call along with the nonzero entries of the matrix:
n = 3;
a = 0.2;
b = 0.5;
c = 0.8;
circuit = tridiag_cab(n, a, b, c);
circuit.draw; ┏━━━┓ ┏━━━┓ ┏━━━┓
q0: ━━━━━┫RY ┣━┫RY ┣━┫RY ┣━━━━━━━━━━━━━━━━━
┗━┳━┛ ┗━┳━┛ ┗━┳━┛
┏━┓ ┃ ┃ ┃ ┏━┓
q1: ━┫H┣━━━○━━━━━○━━━━━●━━━○━○━○━●━●━●━┫H┣━
┗━┛ ┃ ┃ ┃ ┃ ┃ ┃ ┃ ┃ ┃ ┗━┛
┏━┓ ┃ ┃ ┃ ┃ ┃ ┃ ┃ ┃ ┃ ┏━┓
q2: ━┫H┣━━━○━━━━━●━━━━━○━━━○━○━○━○━○━○━┫H┣━
┗━┛ ┃ ┃ ┃ ┃ ┃ ┃ ┗━┛
┃ ┃ ┃ ┃ ┃ ┃
q3: ━━━━━━━━━━━━━━━━━━━━━━━⊕━╋━╋━⊕━╋━╋━━━━━
┃ ┃ ┃ ┃ ┃ ┃
┃ ┃ ┃ ┃ ┃ ┃
q4: ━━━━━━━━━━━━━━━━━━━━━━━○━⊕━╋━●━⊕━╋━━━━━
┃ ┃ ┃ ┃ ┃ ┃
┃ ┃ ┃ ┃ ┃ ┃
q5: ━━━━━━━━━━━━━━━━━━━━━━━○━○━⊕━●━●━⊕━━━━━Pros: easy to use
Cons: limited to symmetric and structured sparse matrices, MATLAB implementation only.
FABLE: Fast Approximate BLock Encodings
From my point of view, FABLE is an enhanced version of the block encoding of sparse matrices with particular structures, which was discussed in the previous section. FABLE is a product of the Quantum Computing Lab research team’s further efforts to make block encoding more practical. Unlike the block encoding of sparse matrices, FABLE can block encode dense matrices without a specific structure. It has been developed using Python and the IBM Qiskit framework, as well as MATLAB and the QSLAB tool. However, it seems that FABLE struggles to encode matrices larger than 128 by 128 in size (unitaries with 7 qubits), based on my observations.
To demonstrate how FABLE works, I have switched to the Python Programming language and IBM Qiskit implementation.
The first improvements I have noticed is that FABLE is supported by PyPI. Hence, it can be easily installed by running
pip install fable-circuitsI recommend utilizing virtual environments such as VENV or Conda or online versions of Jupyter notebooks such as Google Colab or IBM Quantum Lab to install and test various frameworks. Don’t forget to install the Qiskit framework, if necessary, using
pip install qiskitI then import the FABLE and the Qiskit simulator:
from fable import fable
import numpy as np
from qiskit import Aer
simulator = Aer.get_backend("unitary_simulator")Example 3.
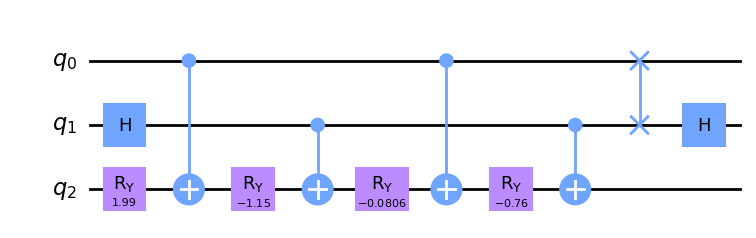
As an example, I will block encode the 2-by-2 matrix A
Note that this matrix is not normalized. Nevertheless, FABLE can handle such matrices automatically and will re-scale matrix A.
To call fable() function, I need to pass in matrix A as a numpy array. The fable() function yields two outputs: the quantum circuit representing the matrix block encoding and the block encoding factor 𝛼.
A = np.array([[3.0, 1.0], [2.0, -1.0]])
circ, alpha = fable(A)
circ.draw(output='mpl')As you can observe from the three examples, the block encoding of a matrix is represented as the sequence of CNOT gates, rotation gates, several Hadamard gates, and SWAP gate(s).
In my article Math Perspective on Block Encoding, I mentioned the impossibility of implementing block encoding of a matrix accurately. In practice, it’s not always possible to achieve perfect block encoding, which is why FABLE allows users to submit an optional parameter called epsilon which represents the absolute error on the matrix block encoding.
To approximate the block encoding of a matrix, FABLE uses a so-called threshold value for parametrized quantum gates (such as Ry(), for example). The threshold allows to ignore angles for parametrized gates smaller than a certain value, which leads to the rotation angles being ignored as well. Additionally, FABLE employs the Walsh-Hadamard domain. This technique allows dense matrices to become sparse in Walsh-Hadamard domain, making block encoding easier to implement.
Pros: easy to use, Python Qiskit and MATLAB implementations, dense matrices support.
Cons: Limited in supporting approximately matrices of 2 to 7 qubit operations.
Xanadu Pennylane Framework
Now, I would like to guide you through Xanadu Pennylane, a machine-learning library for quantum computation, which is my favorite framework for block encoding. Xanadu’s Team has recently added several functionalities related to QSP, QSVT, and block encoding, making them the leading experts in these concepts in Quantum Computing industry, so far. If you would like to learn more about using Xanadu’s Pennylane for block encoding, I suggest checking out the following tutorial by Xanadu’s Team.
Don’t forget to install Pennylane library using pip install:
pip install pennylaneExample 4.
For my next example, I will block encode the same 2-by-2 matrix as in Example 3 but with the aid of the Pennylane BlockEncode functionality. Similar to FABLE, if I input an unnormalized matrix A, Pennylane automatically normalizes it. However, it uses a different from FABLE normalization rule where the original matrix is divided by the expression ||AA^*|| or ||A^*A||, whichever is larger. Here, A^* is a complex conjugate of A. So, don’t be surprised when studying these frameworks more in-depth, you will discover different versions of normalized matrices.
Next, I import Pennylane library, define the matrix to be block encoded, and a quantum device:
import pennylane as qml
A = np.array([[3.0, 1.0], [2.0, -1.0]])
dev = qml.device('default.qubit', wires=2)As as a last step, I use the BlockEncode class to define the block encoding and pass the matrix A as an argument
@qml.qnode(dev)
def block_encoding():
qml.BlockEncode(A, wires=range(2))
return qml.state()That was it 😇. If I print out the block encoding, I find the normalized version of matrix A embedded in the top left corner:
[[ 0.2 0.06666667 0.97745988 -0.01130199]
[ 0.13333333 -0.06666667 -0.01130199 0.98876187]
[ 0.97067869 -0.0022604 -0.2 -0.13333333]
[-0.0022604 0.99554307 -0.06666667 0.06666667]]Note that a matrix block encoding is not unique. If you are getting a different result from mine when playing with the number of qubits or other parameters, your answer is still correct.
Pros: block encode in one line of code, use a matrix block encoding to run quantum algorithm immediately.
Cons: Not discovered yet, or maybe I am biased 😅.
References
When preparing this article, the results of the following scientific works and tutorials have been used:
Diego Guala, Jay Soni, Soran Jahangiri, “Block Encoding with Matrix Access Oracles” (tutorial), 2023.
All opinions and views are my own and do not reflect opinions of my current, past, or future employers. During the process of writing this article, I was not associated with any of the academic labs or companies mentioned.